混合精度Krylov部分空間法による連立一次方程式の求解について (前編)
20201217追記:よくよく読み返してみるとタイトルが「混合精度」なのに話してることが「高精度」だけで精度を混ぜる話なんにもしてないことに気づいたのでこっそり「前編」だったことにしました.後編は今度書きます.
はじめに
この記事は数値計算 Advent Calendar 2020の16日目の記事です.
みなさん連立一次方程式解いてますか?
この研究は脳筋マゾヒストが何も分からずにKrylov部分空間法という闇を殴り続けている過程について書きます.
本記事では連立一次方程式解法の1つのカテゴリであるKrylov部分空間法と, Krylov部分空間法を高精度演算で行うことについて扱います.
高精度と聞いて円周率みたいな細かい桁のシミュレーションと思った方, そういう話じゃありません. 本記事ではみなさんが普段やるような1.0e-8とかの近似解を求める場合に高精度演算を使うと良さそうだ.という話をします.
なお,
- Krylov部分空間法の詳しい説明はしませんので詳しいことが知りたい人はSaad大先生の本を読んでください(PDF落ちてます)
- 作成者はHPCと高精度演算の人なので理論方面の説明はざっくりです
- このブログでmathjaxを使うのが初で苦戦してます.数式周りは心の目で見てください
- 最後まで読んでも高精度演算でKrylov部分空間を実装すると便利だなあ!とはなりません.僕の苦しみが共有されるだけです.応用研究に協力してくれる人を募集しています
- この記事は個人として書いているので所属とは関係ない
- Qiitaが嫌いなので個人サイトに書いてますが,コメント等あったらTwitterかメールなりで頂けたらと思います
それでは本編を始めます.
連立一次方程式 $$ Ax = b $$ の求解アルゴリズムは様々なものが提案されています.
(mathjax使えた~よかった~設定疲れた~)
最も有名なものは直接解法に分類されるLU分解 (ガウスの消去法)かと思います.
これはN*Nの行列に対して, \[{2 \over 3}N^3 (後退代入を含む) \] の計算量で求解できる優れたアルゴリズムです.
一方で多くの物理シミュレーションで現れる偏微分方程式などを差分法や有限要素法などを用いて離散化することによって得られる行列は疎行列 (行列の要素がほとんどゼロの行列)です.
疎行列は解析領域を格子分割するなどによって得られ,解析領域を細かく分割することによって離散化誤差を減らし精度の高いシミュレーションを行えますが,行列のサイズは大きくなり求解にかかる時間が増大します.
一般的に離散化により得られる疎行列は格子点数に依存した次元数および各格子点の節点間の接続に依存した非零要素をもつため, このとき1行あたりの非零要素は変わらず,行列の次元数だけが増えていくことが多いため,行列の密度はどんどん減っていきます.
※ 1行あたりの非零要素数は元の問題にも依存しますが,多くて100くらいが一般的に思います (例外はいくらでもありますが).
そのためN*N行の行列全体の非零要素数は100N程度しかないような行列になります.
※ 実際にこのような行列がどのようにして現れるかについては@nqomorita氏が数値計算Advent Calendar 2018で書かれた 有限要素法と反復法線形ソルバのはじめの一歩[前編]などを読んでください (仕事が明らかに忙しいのは知ってますが後編楽しみに待ってます!)
話を戻すとこのような疎行列はメモリ使用量を節約するために行番号や列番号のインデックス配列を用いて零要素を記憶しない格納形式を用います (詳しくはCRS形式などを調べてください).
このような疎行列のメモリレイアウトを用いた場合,後から値を挿入(fill-in)したり列方向にアクセスしたりするのが非常に面倒です.
気軽な気持ちで行列行列積なんかした日には結果として密行列が出てくるので台無しです(疎×疎は疎とは限らない).
そのため疎行列を係数とする連立一次方程式解法では疎行列の値の書き換えや挿入が頻繁に行われるLU分解などの直接解法でなく反復解法がよく使われます. (なお,マルチフロンタル法など疎行列を疎のままでLU分解する手法もありますが,それについては触れません)
Krylov部分空間法と共役勾配法
Krylov部分空間法は,
連立一次方程式$$Ax = b$$ に対する
初期近似解x_0に対応する初期残差ベクトル
$$ r_0 = b - Ax_0$$ を用いて
Aのべき乗とr_0の積の像が張る空間から近似解を探索する反復法アルゴリズムの一つのカテゴリで,
行列の性質に応じて様々なアルゴリズムがあります.
ここで理屈について説明してると大変なので,何となく行列をかけたり,ベクトルの内積取ったりしてるんだな.程度の理解をしていただければOKです.
どういう理屈なのかについては日本語なら 前原先生のスライドや山本先生のスライド
などを見てください.
また,Krylov部分空間にはLanczos法やArnoldi法のように連立一次方程式解法だけでなく固有値解法なども含まれます.
共役勾配法
Krylov部分空間法の代表的な連立一次方程式解法に共役勾配法 (CG法)があります. もう数式を書くのに疲れてきたのでWikipediaの共役勾配法のページから拾ってきた画像を引用します.
図1 共役勾配法のアルゴリズム (出典:Wikiperia)
一般的にアルゴリズム中の残差ベクトルr に対する相対残差ノルムが十分に小さくなるまでこれを繰り返します.
共役勾配法は理論上はN回で収束することが知られています.
つまり計算量について考えてみると,
- ループ中に現れる行列
Aへの計算はAp_kの計算だけ(2回出てくるけど使い回せばいいので1回) xやrに対する内積やらベクトル和やらが10回くらい- 行列
Aは更新されない (コードの左辺に来てないでしょ?)
なので,行列 A の次元数がNで,非零要素数が nnz 個だとすると,
- 行列ベクトル積
Ap_kの計算量はnnz - 内積などは10回*N
くらいです.仮に1行あたりの非零要素数を100とすれば,
(100N (行列ベクトル積) + 10N (ベクトル演算)) * N (反復)
ということで110N^2くらいの計算量で求めることができて,2/3N^3かかるLU分解よりも少なく済みます (なおSparse直接解法は本記事ではry).
しかし, Krylov部分空間法って最高じゃん!もうLU分解なんて窓から投げ捨てようぜ!!!とは残念ながらなりません.
P.S. 疎な構造なのに密行列で持つなんて発想は窓から投げ捨ててください
問題について語っていきます.
Krylov部分空間法の問題点と高精度演算
Krylov部分空間法はN回で必ず収束すると言ったな.あれは嘘だ
N回というのは理論上の話で,これは無誤差な場合に限定されます (ここで誤差とは丸め誤差を指す).
一般的に収束判定は1.0e-8とかにすることが多いのですが,問題規模や条件によって内積や行列積を繰り返すうちに誤差が蓄積していつまでも収束しない現象が起きます. N回以上に回していれば解けるケースもあれば,一生解けない場合(停滞)や,どっかに値が吹っ飛んでいく(発散)ケースもあります.
つまり残差の判定がアキレスと亀状態になったり,しまいにはどこかに吹っ飛んでいったり,循環してしまったりするということです.
計算機の発展,つまり演算性能やメモリサイズが増大に伴って,扱われる問題の規模が大きくなってきており丸め誤差による収束への影響も増大しています 出典(PDF).
そのため,今まで解けていた解析対象であったとしても規模を大きく(メッシュを細かく切るなど)によって急に解けなくなったりする可能性があります. (内積するベクトルのサイズが増加→誤差もより蓄積)
ああなんて恐ろしいんでしょう.
これに対して前処理をしたり,アルゴリズム自体を改良したりといった工夫によってアルゴリズムの収束性を高めたりする研究が盛んに行われています.
しかし,アルゴリズムを変えたところで解けるかどうかわからないとか,数学的に同じことをやっているのかとか,まぁいろんな問題がつきまといます.
これを解決する手法の1つが高精度演算です.
つまり誤差が問題であるならば桁を上げて誤差を吸収してやろうという力技です
LAPACKチームの調査によると,16%のユーザーがよくまたは時々高精度を使っているらしいです (原典がわからないけど出典はこちら).
それではこれを見て感動してください!!!!!
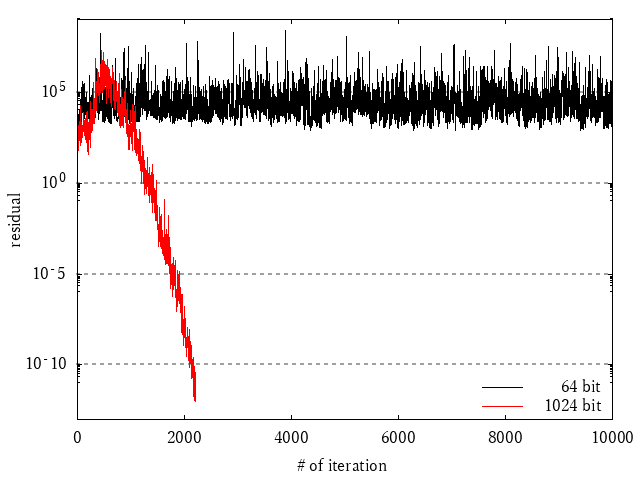
図2 ある問題における収束履歴の例1
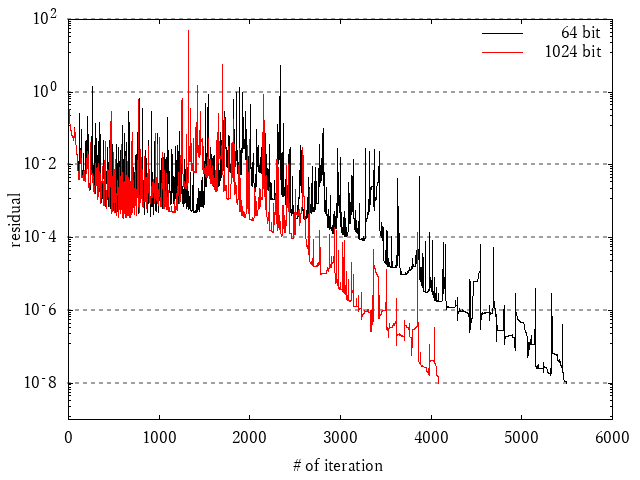
図3 ある問題における収束履歴の例2
これはある2つの問題を相対残差1.0e-12になるまでCG法で解いた結果をプロットしたものです.
黒が64bit(倍精度)で,赤がGMPによる1024 bitの結果です.(GMPについては過去の記事もよろしくね)
この図では横軸が反復回数,縦軸が相対残差で,下の方に最初にたどり着いた人が勝ちという単純なグラフです.
なんと!!!!高精度演算が圧勝しました!!!!!!
きっとより精度の高い解を得たり解けない問題を解けるようになります!!!!
\大勝利!!!!!!/
お わ り
制作・著作
━━━━━━
ⒽⓅⒸ
そんなわけあるかい
高精度演算の問題点
私としては前の章で終わりたかったですが,ここからが問題です.
確かに高精度演算を使えば,
- 解けない問題が解けたり
- 少ない反復回数で計算が終わったり
することがわかりました.
前の章では示しませんでしたが,1024 bitでは更に進めていくと相対残差がもっと小さい(精度の良い)答えまで求めることができます.
この時点で,
- 既に倍精度では解けないことがわかっていたり,
- 倍精度では表現できないくらい精度のよい答えが知りたい
という人には有益でしょう.
しかし,
計算機の発展,つまり演算性能やメモリサイズが増大に伴って,扱われる問題の規模が大きくなってきており丸め誤差による収束への影響も増大しています 出典(PDF). そのため,今まで解けていた解析対象であったとしても規模を大きく(メッシュを細かく切るなど)によって急に解けなくなったりする可能性があります.
こちらのニーズとしては微妙です.なぜならGMPは遅いからです.
64 bitと1024 bitでは1反復あたりの計算時間が100倍くらい違います つまり横軸の"1反復"のコストが違うのです.
さらに1024 bitに増やしたことでメモリも大量に使います. また,今回使った1024bitというのは適当な数字で,本当にユーザが使うアプリケーションで1024 bitで十分なのかは分かりません. もしかすると10,000 bitくらいないとダメなのかもしれません.
また,最初に直接解法(LU分解)を否定しましたが,直接解法であれば必ず解けるのです. 10,000 bitも使うくらいなら密行列として持ってLAPACKなりに突っ込んだほうがマシかもしれません. (直接法も蓄積誤差はありますが...それは精度保証の人などの論文を読んでください..そっちに興味がある方はkvライブラリなど使ってみると良いんじゃないでしょうか)
もっと言えば,不完全LU分解などの収束性の高い前処理を使ったほうが全然良いかもしれません(前処理については各自調べてください).
ということで,精度を上げるという1つの改善策としては有効性は示されましたが, 実アプリケーションにおける応用としては疑問が残ります.
ここからは実アプリケーションに向けた私の研究について紹介していきます. ただし,実際に実アプリケーションに応用できるという結論にはたどり着きません.最後はポエムです.
応用に向けた検証と,ポエム
私の研究:DD演算の高速化について
私の研究は,実アプリケーションで実用的に高精度演算という「改善策」を選択肢の一つとして選べるようにすることです.
そのためのアプローチとして,まずは倍精度の2倍の精度の128 bitの演算の高速化と,C++から標準型のように使うためのインタフェースの開発をしています.
これらの成果は
DD-AVX_v3
として公開されており,こっちの記事に詳しく書きましたので,良ければ見てください.
あと,githubにスターなど頂けたら励みになるのでよろしくおねがいします.
最近ではこれらの成果をいくつかの研究会などで報告しており,見ていただいた方もいるかも知れませんが, 128 bitのDD型でも倍精度と比べて1.2~1.5倍くらいの時間で計算ができるようなライブラリになっています.
反復回数の変化についてはもっと実問題の応用を積み重ねて有効な適用範囲を見つけていくつもりですが, 仮に反復回数が変わらなくても1.5倍程度の時間の増加で済みます.
倍精度を使って解けなかったときのリスク回避に払うコストが1.5倍というのは,悪くない賭けじゃないかと思いますので, よかったら使って感想をいただけたら幸いです.
精度を変えると何が起きているのかのポエム
ここで終わっておけばよかったんだよこの記事
でも書きたかったんだよ.
読者の皆様,ここでブラウザを閉じれば気持ちよく終われます
さて,1反復の時間が1.2~1.5倍なら反復回数を70%くらいまで減らせれば高精度なのに倍精度より速く(しかも解ける確率も高く)なるんじゃね? という欲が出てきました.
そうなると事前に高精度化の効果がどのくらいなのかを自動で判定したいなどの欲も出てきます.
よーし傾向を調べるぞ~~!!!と思い,1000問くらいの問題をバカみたいにスクリプトで解いてみました.
行列データはSuite Sparse Matrix Collectionという行列コレクションから大きい順に全部引っ張ってきました.
先程までとは違うのですが対称と非対称を区別せずに行列を引っ張ってきたので,非対称でも解けるBiCGSTAB法というアルゴリズムで解きました.
倍精度と128 bitで1000問解いたところ,
- 解けなかった問題が433問
- 反復回数が128 bitにしたことで1回でも減ったケースは529問
- 反復回数が変わらなかったケースは36問
- 反復回数が増えたケースは2問
でした.
倍精度とくらべて倍々精度のほうが速いケースもありました.ただケーススタディ止まりなので紹介はやめておきます.
行列は何も考えずに引っ張ってきてるので,解けなかった433問は数学的にBiCGSTABでは解けなかったのかもしれません.分母から省くべきでしょう. そうすると567問のうち収束が多少なり改善したのは93% です.
いや~~~よかった~~~~
反復回数が増えたケースは2問
「反復回数が増えたケースは2問」
「「「反復回数が増えたケースは2問」」」
なにこれ???????
は???????????
犯人のうち1人はepb1とかいう名前の行列でした.
64, 128, 256, 512, 1024 bitそれぞれで解いたときの収束履歴を以下に示します.

図 4 epb1のBiCGSTAB法の収束履歴
見てください倍精度が一番早く(もちろん速く)解けるのです
全く意味が分かりません.
この問題について詳しく見てみます.
以下のグラフは,BiCGSTAB法のalphaという変数を,1024 bitを真値だと思って各反復で相対誤差をとったものです.

図 5 epb1で1024 bitを真値としたalphaの相対誤差
この結果から,最初のうちは精度を上げるとちゃんとalphaが1024 bitに近い (精度の良い)値になっていることが分かりますが, 400反復もすると誤差が積もるらしく訳がわからない事になっているようです.
数値が悪すぎるのか?桁落ちでもしてるのか?
とにかく最終的に運が悪くて反復回数が増えるようです.
じゃあちゃんとDDにして収束が改善したやつではどうでしょうか?
comsolという行列も見てみます.

図 6 comsolのBiCGSTAB法の収束履歴
- ご覧の通り反復回数は減っていて,倍精度だけが遅い結果です.
- 128~1024 bitは同じような収束履歴になっていることが分かります.
ではalphaの値はどうでしょうか?

図 7 comsolで1024 bitを真値としたalphaの相対誤差
全くズレています.
ちなみに「収束した」と判定されたときのalphaの値はそれぞれ
- 64 bit: 3.13E+00
- 128 bit: 2.04E-01
- 256 bit: 2.17E+00
- 512 bit: -9.16E+01
- 1024 bit: -9.16E+01
となっていました.128 bitだと-0.2で1024 bitだと-91.6です.どうして同じような収束履歴をたどったんでしょうか?
何を見れば良いのかさっぱり分かりません.ちなみにどれも収束はしています.
b-Ax してみてもちゃんと答えはあっているようです.
無誤差な状態で少なくなるのは分かるのですが,64 bitと128 bitくらいだとどこが良くなったのか見つけるのがなかなか難しく,今回の分析はここまでにしました.
誰かこれの分析方法についてアイデアがある人は教えて下さい.
おわりに
皆さんが普段楽しく使っているKrylovがマジで訳がわからない話をしました.
一方で高精度演算の有用性については分かって頂けたのではないでしょうか.
高精度演算をつかってKrylov部分空間法の収束を改善することの強みはアルゴリズムの並列性を崩さないことにあります. 本文ではあまり触れませんでしたが,ILUなどの並列度の低いアルゴリズムはGPUなどでは性能が出ないですが,そういったアルゴリズムを使わずに収束性を改善することができます.
Krylov部分空間法を使う上で現状のパラメタは「解法」と「前処理」ですが,そこに「精度」を加えることで,新しい世界が拓けるのではないかと思っています.
プログラム自体は簡単なものですし,天才的な数学的才能が求められている研究でもないと思います. あまり掘られていない分野なので,興味を持った方がいたら是非連絡いただけたらと思います.
また,本文では触れませんでしたが最後の結果についてどういう比較方法をすればいいのかには疑問が残ります. ただ,この実験をするのにかなりの手作業が入っていて,高精度な数をファイルI/Oするとよく分からんので,1024 bitを1反復して値を取ってきて同じプログラムの中で比較したりと,かなり面倒なことをしました.
精度を自在にコントロールしたり,複数の精度でプログラムをはしらせ,gdbみたいな感じで対話っぽく精度を比較できると精度検証がしやすいのですが, 中々そういう環境がないのがつらいところですし,どうやって作るかというのも難しい問題です.
結論として現状では訳が分からなかったわけですが,収束と精度の関係を調べる話は沼なので置いておくとしても, また,精度を上げてゴリ押しすれば解けることはご理解いただけたんじゃないでしょうか.
精度を上げて収束を安定させることのメリットは,アルゴリズムを変えなくて良いことだけでなく,元のアルゴリズムの並列度を維持できるということにもあります. GPUなどでILUなどの並列性の低い前処理をするのはどうしても難しいですが,精度に関しては並列度に寄与しないので,高い並列度を維持したままで収束性をコントロールすることが出来ます. そのため,精度の高い演算を使えるプログラムというのは1つ持っておいても良いんじゃないでしょうか.
最後にCMですが,私は所属している科学計算総合研究所で FOCUSにおけるFrontISTRのサポートや, A64fx, SX-Aurora TSUBASA, GPUなどにおけるFrontISTRの高速化を担当しています.
これらの並列化環境においては前述の通り前処理アルゴリズムの並列性が課題となってくるため, 弊社では大規模・悪条件な構造解析に対して高精度演算を使って高い並列度で計算するアルゴリズムを開発し, FrontISTRへの組み込みなども行っています.
通常では倍精度かつCPUでしか動かないFrontISTRを高速なアクセラレータや高い精度で動かしたいというご要望のある方は連絡いただけたら私ががんばります. また,FOCUSのリンクにある機械学習による設計フローの加速についても是非よろしくお願いします.

